সংখ্যাদের নিয়ে গল্পটা প্রায় লোকগাথায় পরিণত। রামানুজন অসুস্থ হয়ে লন্ডন থেকে কিছুটা দূরে পুটনি শহরতলিতে একটা নার্সিংহোমে ভর্তি। তাঁকে দেখতে গেছেন কেমব্রিজে তাঁর মেন্টর অধ্যাপক গডফ্রে হ্যারল্ড হার্ডি। কেবিনে ঢুকেই রামানুজনকে বললেন, “জানো রামানুজন, আমি যে ট্যাক্সি চেপে এখানে এলাম, তার নম্বর ১৭২৯। সংখ্যাটা কেমন যেন বড় সাদামাটা, আকর্ষণহীন।” রামানুজন শুনেই বলে উঠলেন, “না, না হার্ডি। ১৭২৯ সংখ্যাটা বেশ আকর্ষণীয়। আসলে এটা হল সেই ক্ষুদ্রতম সংখ্যা, যাকে দুটো পূর্ণঘন (Cube) সংখ্যার সমষ্টি আকারে দুরকম উপায়ে প্রকাশ করা যায়।” উদাহরণ দেওয়া যাক -

১৭২৯ = ১০^৩ + ৯^৩  = ১২^৩ + ১^৩
৪১০৪ = ১৬^৩ + ২^৩ = ১৫^৩ + ৯^৩
১৩৮৩২ = ১৮^৩ + ২০^৩ = ২৪^৩ + ২^৩
... = ... + ... = ... + ...

অবশ্যই কোনো ঋণাত্মক সংখ্যা এখানে আলোচনায় ধরা হয়নি। যেটা গুরুত্বপূর্ণ তা হল ১৭২৯, ৪১০৪,  ১৩৮৩২, ... এ-ধরণের সংখ্যাদের মধ্যে ১৭২৯ ক্ষুদ্রতম।    

রামানুজনের তাৎক্ষনিক উত্তরে হার্ডি বিস্ময়ে হতবাক। এপ্রসঙ্গে বলে রাখা যাক, হার্ডি নিজেও একজন  বিশ্ববিশ্রুত নাম্বার থিয়োরিস্ট। সংখ্যাদের নিয়ে রামানুজনের অন্তর্দৃষ্টি আবার একবার তাঁকে মুগ্ধ করল।  ১৭২৯ সংখ্যাটি দুরূহ গণিতের কুহকজাল ভেদ করে ‘হার্ডি-রামানুজন সংখ্যা’ বা ‘ট্যাক্সি-ক্যাব সংখ্যা’ নামে জনমানসে পরিচিত হয়। ‘১৭২৯’ এর জনপ্রিয়তা আমেরিকার বিখ্যাত টেলিভিশন নেটওয়ার্ক ‘ফক্সে’র কল্প-বিজ্ঞান কমেডি ধারাবাহিক ‘ফুটুরামা’কে প্রভাবিত করে। ১৯৯৯ সাল থেকে প্রচারিত এই আ্যনিমেটেড কার্টুন সিরিয়ালে কখনও রোবট ‘বেন্ডার’-এর নম্বর হয় ১৭২৯, কখনও বহু-বিশ্বের কল্পনায় কোনো একটা বিশ্বের নাম দেওয়া হয় ‘ইউনিভার্স-১৭২৯’, আবার কখনও স্টারশিপের রেজিস্ট্রেশন নম্বর হয় ‘বিপি-১৭২৯’। আমেরিকান ড্রামা ফিল্ম (২০০৫) ‘প্রুফ’-এ মুখ্য চরিত্র রবার্ট, এক খ্যাপাটে ব্রিলিয়ান্ট গণিতজ্ঞ। তাঁর জবানিতে উঠে আসে ‘হার্ডি-রামানুজন সংখ্যা’র রহস্য। কোনো বিশেষ সংখ্যাকে ঘিরে সাধারণ মানুষের এই উন্মাদনা, আবেগ বাস্তবে বিরল।            

আরও পড়ুন
রামানুজন-গ্রাফ সমাধান করে ‘মাইকেল অ্যান্ড শিলা হোল্ড পুরস্কার’ জয়ী ভারতীয় গবেষক

ভারতীয় গণিতবিদ রামানুজনের উত্তর কি সত্যিই তাৎক্ষণিক ছিল? না, ইংল্যান্ডে আসার আগে থেকেই তিনি এ-জাতীয় সংখ্যাদের নিয়ে চর্চা করেছেন। কোনো সময় নোটবুকে লিখেও রাখেন। আর তা কোনোভাবে রয়ে যায় তাঁর স্মৃতির গহন কুঠুরিতে। আজ আবার কোনো অতীন্দ্রিয় সংকেত খুলে দিয়েছে সেই কুঠুরির দ্বার।

আরও পড়ুন
পরিবারের মধ্যেই গণিত নিয়ে রেষারেষি, বার্নৌলিদের সঙ্গে জড়িয়ে অদ্ভুত ইতিহাস

‘হার্ডি-রামানুজন সংখ্যায় কীসের সংকেত?   

আরও পড়ুন
জার্মান কোড সমাধান করে দ্বিতীয় বিশ্বযুদ্ধকে চার বছর কমিয়ে দেন এই গণিতবিদ

শখের গণিতজ্ঞ ফরাসি আইনজীবী ফার্মা (ফারমাট উচ্চারণও করা হয়) অবসর সময়ে গণিতচর্চা করতেন। তাঁর অদ্ভুত অভ্যাস ছিল। খাতার মার্জিনে বা বইয়ের মার্জিনে অঙ্কটি সম্পর্কে সমাধান বা সমস্যা ছোটো নোট আকারে লিখে রাখতেন। দিওফান্তাসের লেখা ‘এরিথমেটিকা’ বইটি ফার্মার খুব প্রিয় ছিল। ফার্মা মারা গেলেন ১৬৬৫ সালের ১২ ই জানুয়ারি। ফার্মার ছেলে বাবার সব গবেষণা একজায়গায় করে ১৬৭০ সালে একটি বই প্রকাশ করলেন। নাম ‘দিওফান্তেস এরিথমেটিকা কন্টেনিং অবজারভেশন বাই পীয়ের দ্যা ফার্মা’। বইটিতে দেখা গেল একজায়গায় মার্জিনে নোট। xⁿ + yⁿ = zⁿ সমীকরণটিতে n  এর ২-এর বেশি মানের জন্য কোনো ধনাত্মক পূর্ণ সংখ্যা x, y, z পাওয়া যাবে না। উল্লেখ করে ফার্মা  মন্তব্য জুড়লেন, “আমি এর একটা দারুণ সমাধান জানি, কিন্তু মার্জিনে জায়গা এত কম, যে তা এখানে  ধরবে না।” উপপাদ্যটি ‘ফার্মার শেষ উপপাদ্য’ নামে পরিচিত হয়। সাড়ে তিনশো বছর ধরে গণিতজ্ঞরা ফার্মার দুর্বোধ্য ধাঁধাঁর সমাধান খুঁজেছেন। অবশেষে ১৯৯৫ সালে আমেরিকার প্রিন্সটন বিশ্ববিদ্যালয়ের ব্রিটিশ গণিতজ্ঞ অ্যান্ড্রু উইলসের দুবারের প্রচেষ্টায় তা সমাধান হয়।

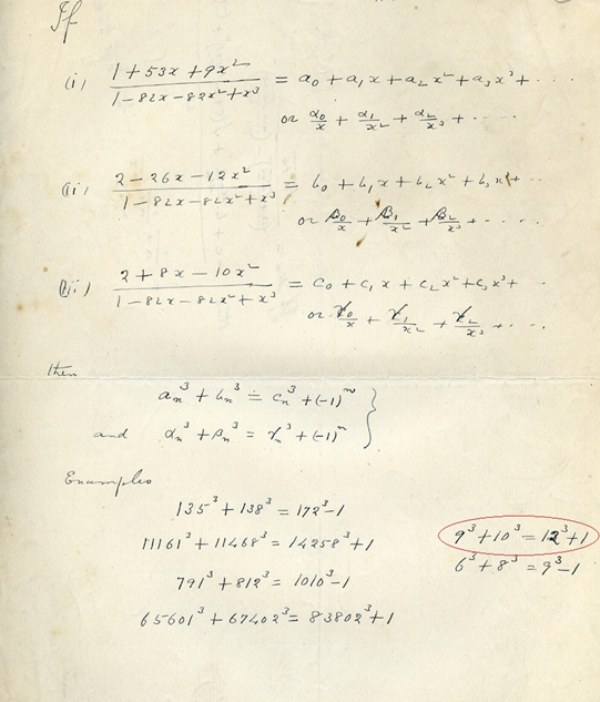রামানুজনের নোটবুকের পাতা থেকে

 

রামানুজন ইতিমধ্যেই অয়লারের ডায়োফান্তাইন সমীকরণ x³ + y³  = z³ + w³ এর সঙ্গে পরিচিত ছিলেন। আধুনিক গণিতে যা কিউবিক সারফেসের ধারণা দেয়, যা প্রকৃতপক্ষে একটি র‍্যাশনাল ইলিপটিক সারফেস। অয়লারের সাধারণ সমাধানের সমতুল একটা সরল সমাধানগুচ্ছ রামানুজন দিয়েছিলেন। যা ইলিপটিক কার্ভের (সারফেস) অসীম সংখ্যক বহু (infinitely many) সমাধানের খোঁজ দেয়। রামানুজনের মৃত্যুর ৩৮ বছর পর ১৯৫৮ সালে অ্যান্ড্রু উইলস কিউবিক সারফেসের এক বিশেষ গঠনকে নাম দেন K3-সারফেস। রামানুজন নিজের অজান্তেই এই K3-সারফেসের হাত ধরে প্রায় পৌঁছে গিয়েছিলেন ‘ফার্মার শেষ উপপাদ্য’-র জটিল সমাধানে; অন্তত, যেখানে n এর মান ৩। ২০১৬ সালে ‘রিসার্চ ইন নাম্বার থিয়োরি’ জার্নালে প্রকাশিত একটি গবেষণাপত্রে বিখ্যাত নাম্বার থিয়োরিস্ট কেন ওনো এবং তাঁর ছাত্রী সারা ট্রেবা লেডার দেখান কিভাবে ‘হার্ডি-রামানুজন সংখ্যা’র সূত্রে রামানুজন তাঁর মৃত্যুশয্যায় যে ফর্মুলা নোটবইতে লিপিবদ্ধ করেন, আসলে তা ইলিপটিক কার্ভের গূঢ় সংকেত। ইলিপটিক কার্ভ শুধু যে গণিতের চর্চার বিষয়, তা নয়। ব্যবহার হচ্ছে ইন্টারনেট ক্রিপ্টোগ্রাফিতে; যা ব্যাংক অ্যাকাউন্টের গোপনীয়তা রক্ষা সহ ইন্টারনেট ব্যাঙ্কিংয়ের পাসওয়ার্ডেরও সুরক্ষা দেয়। প্রিন্সটন  ইউনিভার্সিটির ভারতীয় বংশোদ্ভূত অধ্যাপক ও নাম্বার থিয়োরিস্ট মঞ্জুল ভার্গব বলেন,  “রামানুজন এক বিশেষ ধরনের K3-সারফেস চিহ্নিত করেছিলেন, যা ইলিপটিক কার্ভের এক বিশেষ ফ্যামিলিকে বুঝতে সাহায্য করে।” ওনো আরও পরিষ্কার করে বলেন, “রামানুজন ১৭২৯ এবং ইলিপটিক কার্ভ ব্যবহার করে এক বিশেষ ধরনের K3-সারফেসের জন্য গাণিতিক সূত্র নির্ণয় করেছেন।” যে কিউবিক সারফেসের ধারণা আজ বিশুদ্ধ গণিতের পরিমিত আঙিনা ছাড়িয়ে স্ট্রিং থিয়োরি ও কোয়ান্টাম ফিজিক্সের গাণিতিক ব্যাখ্যায় ব্যবহৃত হচ্ছে। স্ট্রিং থিয়োরি আজ ‘থিয়োরি অফ এভরিথিং’-এক গাণিতিক মডেল যা কৃষ্ণগহ্বর, বিশ্বব্রহ্মাণ্ডের সৃষ্টি রহস্য ব্যাখ্যা করছে।

ইলিপটিক কার্ভস

সংখ্যাদের নিয়ে রামানুজনের এহেন অন্তর্জ্ঞান লক্ষ্য করে কেমব্রিজে হার্ডির সহকারী গবেষক ও অধ্যাপক  লিটলউড একবার বলেছিলেন, “প্রত্যেকটি সংখ্যা যেন রামানুজনের ব্যক্তিগত বন্ধু।” রামানুজন বিশেষজ্ঞ কেন ওনো-র মতে, “রামানুজনের নোটবইগুলোর পাতা ওলটালে যেটা অতি সাদামাটা একটা ফর্মুলা বলে মনে হয়, খুব ভালো করে নিরীক্ষণ করলে তা থেকে গভীর তাৎপর্যপূর্ণ কোনো গাণিতিক ধারণার জন্ম হতে পারে। আর এটাই রামানুজনের গণিতের আসল শক্তি।”

Powered by Froala Editor